Heron's Formula ⇒⇒ Exercise 10.1

Question 1

A traffic signal board, indicating 'SCHOOL AHEAD', is an equilateral triangle with side ‘a’.
Find the area of the signal board, using Heron's formula. If its perimeter is 180 cm, what will be the area of the signal board?

Solution :

We are given that the perimeter of the signal board is 180 cm.

Side of the signal board = a

Since it's an equilateral triangle, all three sides are equal.

Perimeter = a + a + a = 3a

$ 3a = 180 cm $

$ a = 60 cm $

Semi perimeter of the signal board

(s) = $ { { a + a + a } \over 2} $ = $ { 3a \over 2} $

$ s = { { 3 × 60 } \over 2} $

$ s = { 90 cm} $

Using Heron's formula

Area of the signal board $ = {\sqrt{s( s−a)(s−b)(s−c)}} $

$$ {\sqrt{90 ( 90 - 60 ) ( 90 - 60 )( 90 - 60 )}} $$

$$⇒ {\sqrt{90 × 30 × 30 × 30} } $$

$$⇒ {900√3} $$

$⇒ {900√3} $ $cm^2$

The area of the signal board = $ {900√3} cm^2 $

Question 2

The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?

Solution :

We are given as shown in the figure the sides of the triangular side walls of flyover .

Let the sides of the triangular wall be a = 122 m, b = 22 m, and c = 120 m

First, calculate the semi-perimeter,

Semi perimeter of the signal board (s) = $$ { { a + b + c } \over 2} $$

$$ { { 122 + 22 + 120 } \over 2} $$

$$ = 132m $$

Now, calculate the area using Heron's formula

Area of the signal board $ = {\sqrt{s( s−a)(s−b)(s−c)}} $

$$ {\sqrt{132 ( 132 - 122 ) ( 132 - 22 )( 132 - 120 )}} $$

$$⇒ {\sqrt{132 ( 10 ) ( 110 )( 12 )}} $$

$$⇒ {\sqrt{132 × 10 × 1320 } } $$

$$⇒ {\sqrt{132 × 10 × 132 × 10 } } $$

$$⇒ {132 × 10} $$

$⇒ {1320} $ $m^2$

The area of the signal board = $ 1320m^2 $

Calculate the rent for 3 months.

Rent of advertising per m² per year = Rs 5000

Rent of advertising per m² per month = Rs 5000 / 12

∴ The rent of one wall for 3 months for $ 1320m^2 $ =

$$ ⇒ {{1320 × 5000 × 3} \over 12} $$

$$⇒ {1,650,000} $$

The rent paid by the company for 3 months is Rs 1,650,000.

Question 3

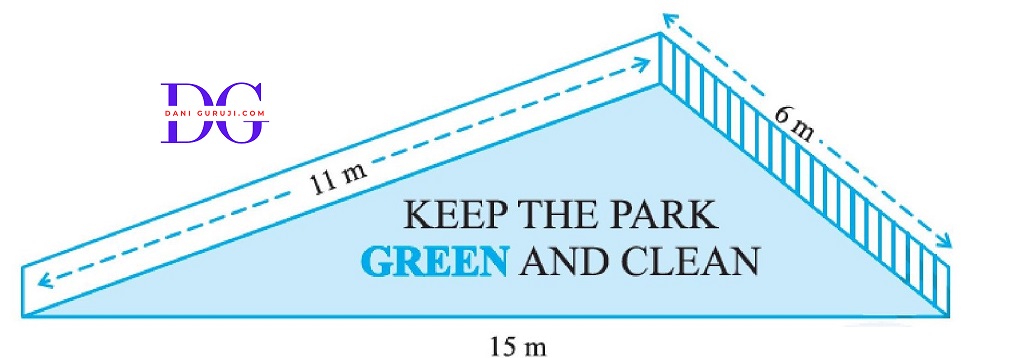
There is a slide in a park. One of its side walls has been painted in some color with a message "KEEP THE PARK GREEN AND CLEAN" (see Fig.). If the sides of the wall are 15m, 11m and 6 m , find the area painted in color.

Solution :

We are given as shown in the figure the sides of the triangular side walls of park .

Let the sides of the triangular wall be a = 15 m, b = 11 m, and c = 6 m

First, calculate the semi-perimeter,

Semi perimeter of the side wall (s) = $$ { { a + b + c } \over 2} $$

$$ { { 15 + 11 + 6 } \over 2} $$

$$ = 16m $$

Now, calculate the area using Heron's formula

Area of the side wall $ = {\sqrt{s( s−a)(s−b)(s−c)}} $

$$ {\sqrt{16 ( 16 - 15 ) ( 16 - 11 )( 16 - 6 )}} $$

$$⇒ {\sqrt{16 ( 1 ) ( 5 )( 10 )}} $$

$$⇒ {\sqrt{16 × 50 } } $$

$$⇒ {\sqrt{800 } } $$

$$⇒ {\sqrt{400 × 2} } $$

$$⇒ {\sqrt{ 20 × 20 × 2} } $$

$$⇒ {20 × \sqrt{2 } } $$

( Taking 20 outside the square root, as a pair is present in square root )

$⇒ {20 × \sqrt{2 }} $ m²

Therefore, the area of the wall painted with the message is = $ {20 × \sqrt{2 }}m^2 $

Question 4

Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm .

Solution :

To find the area of the triangle, we first need to determine the length of the third side.

Given: a = 18 cm, b = 10 cm, and perimeter = 42 cm

Perimeter = a + b + c

( The perimeter of a triangle is the sum of its three sides )

$ 42 = 18 + 10 + c $

$ c = 42 − 28 $

$ c = 14 cm $

Now, First, calculate the semi-perimeter,

( The semi-perimeter is half of the perimeter.)

$$ { 42 \over 2} $$

$$ = 21 cm$$

Now, calculate the area using Heron's formula

Area of the triangle $ = {\sqrt{s( s−a)(s−b)(s−c)}} $

$$ {\sqrt{21 ( 21 - 18 ) ( 21 - 10 )( 21 - 14 )}} $$

$$⇒ {\sqrt{21 ( 3 ) ( 11 )( 7 )}} $$

$$⇒ {\sqrt{21 × 3 × 11 × 7} } $$

$$⇒ {\sqrt{21 × 11 × 21} } $$

$$⇒ {21 × \sqrt{11 } } $$

( Taking 21 outside the square root, as a pair is present in square root )

$⇒ {21 × \sqrt{11}} $ cm²

Thus, the area of the triangle is = $ {21 × \sqrt{11 }}cm^2 $

Question 5

Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm . Find its area.

Solution :

Determine the Actual Lengths of the Sides.

Given: Ratio of the sides = 12: 17 : 25, and perimeter = 540 cm

Let the common multiple for the ratio be x.

Perimeter = a + b + c

( The perimeter of a triangle is the sum of its three sides )

$ 540 = 12x + 17x + 25x $

$ 540 = 54x $

$ x = { 540 \over 54} $

$ x = 10 cm. $

Sides of triangle:

Side a = $ 12 × 10 = 120 cm $

Side b = $ 17 × 10 = 170 cm $

Side c = $ 25 × 10 = 250 cm $

Now, First, calculate the semi-perimeter,

( The semi-perimeter is half of the perimeter.)

$$ { 540 \over 2} $$

$$ = 270 cm$$

Now, calculate the area using Heron's formula

Area of the triangle $ = {\sqrt{s( s−a)(s−b)(s−c)}} $

$ {\sqrt{270 ( 270 - 120 ) ( 270 - 170 )( 270 - 250 )}} $

$⇒ {\sqrt{270 ( 150 ) ( 100)( 20)}} $

$⇒ {\sqrt{(27 × 10) × (15 × 10) }} $ $ × {\sqrt { (10 × 10) × (2 × 10)} } $

$⇒ {\sqrt{(9 × 3 × 10) × (5 × 3 × 10) }} $ $ ×{ \sqrt{ ( 5 × 2 × 10) × (2 × 10)}} $

$⇒ {\sqrt{(3 × 3 × 3 × 10) × (5 × 3 × 10)}} $ ${× \sqrt{ ( 5 × 2 × 10) × (2 × 10)}} $

$⇒ {\sqrt{2 × 2 × 3 × 3 × 3 × 3 } }$ $ {× \sqrt { 5 × 5 × 10 × 10 × 10 × 10}} $

( Taking 2 × 3 × 3 × 5 × 10 × 10 outside the square root, as a pair is present in square root )

$⇒ {2 × 3 × 3 × } $ $ {5 × 10 × 10} $

$⇒ {9000} $ cm²

Thus, the area of the triangle is = 9000cm²

Question 6

An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

Solution :

To find the area of the triangle, we first need to determine the length of the third side.

Given: Length of equal sides of the triangle = 12 cm, and perimeter = 30 cm

Perimeter = a + b + c

( The perimeter of a triangle is the sum of its three sides )

$ 30 = 12 + 12 + c $

$ c = 30 − 24 $

$ c = 6 cm $

Now, First, calculate the semi-perimeter,

( The semi-perimeter is half of the perimeter.)

$$ { 30 \over 2} $$

$$ = 15 cm$$

Now, calculate the area using Heron's formula

Area of the triangle $ = {\sqrt{s( s−a)(s−b)(s−c)}} $

$$ {\sqrt{15 ( 15 - 12 ) ( 15 - 12 )( 15 - 6 )}} $$

$$⇒ {\sqrt{15 ( 3 ) ( 3 )( 9 )}} $$

$$⇒ {\sqrt{15 × 9 × 9} } $$

$$⇒ {9 × \sqrt{15 } } $$

( Taking 9 outside the square root, as a pair is present in square root )

$⇒ {9 × \sqrt{15 } } $ cm²

Thus, the area of the isosceles triangle is = $ {9 × \sqrt{15 } }cm^2 $